Altezze di un triangolo, area e l'ortocentro

In questo file realizzato dagli alunni, qualche mese fa, e modificato in parte da me, si vede il punto di incontro delle altezze di un triangolo.
Questo punto di incontro si dice ortocentro.
Muovendo i punti A, B e C si nota che non sempre l'ortocentro cade all'interno del triangolo, l'ortocentro può essere esterno al triangolo, in tal caso si considerano i prolungamenti delle altezze.
Che cosa succede nel caso di un triangolo rettangolo?
Alcuni degli alunni, ormai abituati a cercare situazioni particolari, hanno notato che se il triangolo è un triangolo degenere le altezze non si incontrano in nessun punto, in quel caso infatti i prolungamenti delle altezze sono paralleli.



Alunni di classe quinta A, 2 maggio 2010 (10 agosto 2016), creato con GeoGebra.

Link:

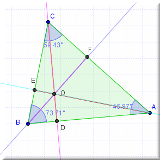Altezze dei triangoli (in questo file si può osservare l'ortocentro in rapporto al tipo di triangolo classificato secondo gli angoli

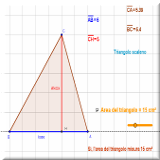Esperienza: un'introduzione all'area dei triangoli

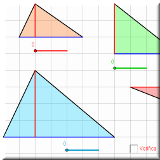L'area dei triangoli (quattro applet in due pagine)