Punti, linee, superfici...
Ci stiamo occupando di punti, linee, superfici, regioni, corpi,
solidi...

Ci è sembrato abbastanza semplice capire che una linea chiusa come
questa che si vede nell'immagine qui sopra divide la superficie in una
parte esterna e in una parte interna.
Nell'immagine sottostante la
regione
esterna è di colore celeste e la
regione
interna interna di colore
arancione chiaro.

I matematici a volte sono... strani e hanno impiegato molto tempo per
dare una dimostrazione per una cosa all'apparenza così semplice.
Ci andò vicino il matematico francese
Camille
Jordan (1838-1922) e la dimostrazione porta il suo nome
teorema
della curva di Jordan.
Insomma i
matematici riuscirono a dimostrare questo nel 1905 e non fu affatto
facile, in seguito pare che abbiano dovuto scrivere ben 6.500 righe per
darne una dimostrazione rigorosa (vedi:
http://it.wikipedia.org/wiki/Teorema_della_curva_di_Jordan).
Abbiamo continuato nel nostro lavoro e abbiamo inserito un punto.
Facile dire che nell'immagine qui sotto
il
punto rosso è esterno alla linea chiusa.
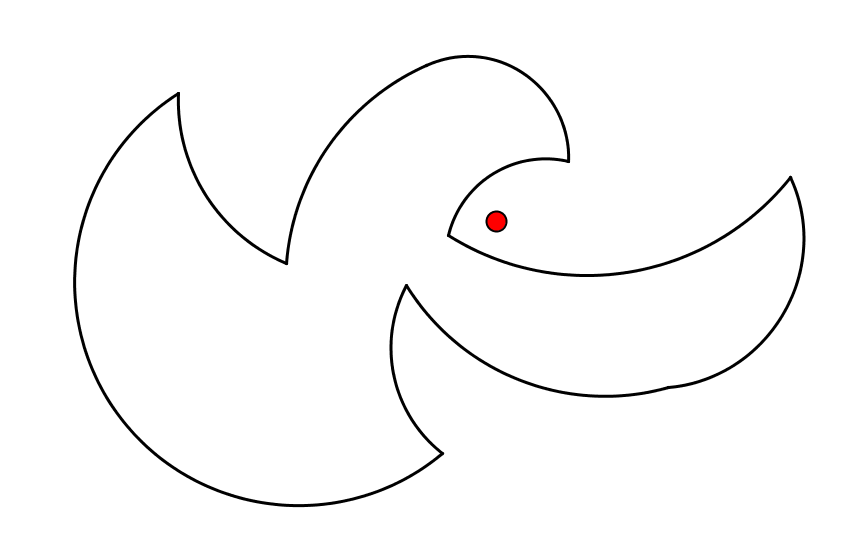
In quest'altra immagine invece
il
punto rosso è interno alla linea chiusa.

È sempre così facile determinare se un punto è
interno o esterno a
una linea chiusa?
Guardate queste immagini. Non sembra proprio semplice farlo a colpo
d'occhio.

Abbiamo provato anche noi a disegnare una linea chiusa complicata, come
questa tracciata da Pietro.
Il punto rosso è esterno o interno?

Le nostre linee
Se fate clic su
questo link, potete scaricare e, se volete,
stampare un
flie pdf con alcune delle linee che abbiamo disegnato.
Osservate le linee: i punti sono esterni o interni?
Qualcuno di voi ha già intuito il
trucco
per saperlo con sicurezza.
Ne riparleremo, per ora: acqua in bocca.
Linea chiusa con GeoGebra
Proviamo a tracciare una linea chiusa con GeoGebra simile a questa
trovata in Wikipedia.

Il video ci spiega come fare.








